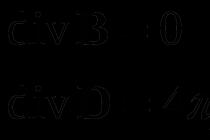Parameters that determine the state of a substance. Ideal gas. Derivation of the basic equation of the kinetic theory of gases. Derivation of basic gas laws. Equation of state of ideal gases.
Ideal gas is a gas whose molecules do not interact with each other at a distance and have vanishingly small sizes. State of given mass m ideal gas is determined by the values of three parameters: pressure P, volume V, and temperatures T.
The ideal gas equation of state or the Mendeleev-Clapeyron equation is a generalization of the ideal gas laws discovered experimentally before the creation of MKT. However, from the basic MKT equation (2.3), one can obtain the equation of state of an ideal gas. To do this, instead of the average kinetic energy of translational motion of a molecule, we substitute the right-hand side of equality (2.4) into the basic MCT equation of ideal gases, and we obtain an equation that does not include gas microparameters (2.5). Since , therefore, or . Considering that , we get N=N A , and since N A × k = R = 8.3 - molar gas constant or universal gas constant, then we get Mendeleev's equation (2.6). The equation of state of a gas is often conveniently used in the notation proposed Clapeyron , if the amount of substance does not change or (2.7). Equation (2.7) is often called generalized gas law . The fact that the equation of state of an ideal gas can be derived from the basic equation of the molecular kinetic theory of an ideal gas confirms the correctness of the molecular kinetic theory of matter.
The basic equation of the molecular - kinetic theory of gases. Let's take a vessel with gas and determine the pressure P gas onto the walls of the vessel. For ease of consideration, let’s choose this vessel in the shape of a cube with an edge l and place it in the Cartesian coordinate system, as shown in the figure. Let there be everything in the vessel N molecules. Let's pretend that:
1) Along the axis X one third of all molecules move, i.e. ;
2) Impact of molecules on the wall Q ideally elastic and the molecules travel a distance equal to the size of the cube without experiencing collisions.
The force impulse received by the wall upon impact of the molecule is determined from Newton's second law. . Where 
- change in the momentum of the molecule, m– the mass of the molecule. Since the mass of the wall is much greater than the mass of the molecule, then 
or modulo, where the notation is used. Thus, one molecule one molecule in time D t transmits a force impulse to the wall 
, and in a time of sec it transmits to the wall a force impulse equal to 
, Where k– number of impacts of molecules in 1 second. 
Since - the time interval between two successive blows,. so then 
. Now let's calculate the total impulse of force that is transmitted to the wall N 1 molecules moving along an axis x, for 1 sec, where the brackets< >denote the average value of the expression in parentheses. If you take the square root of< V 2 >, we obtain the root mean square speed of molecules, which we will denote<V sq.> 
- root mean square speed of gas molecules. The pressure exerted by the gas on the face of the cube is equal to: 
, Where n– concentration of molecules. Let us write this expression in the form 
, to emphasize that the left side of this expression includes the average kinetic energy of the translational motion of the molecule 
. Then 
- the basic equation of molecular kinetic theory (Clausius equation) Taking into account the equation of state of an ideal gas: we obtain an expression for the average kinetic energy of translational motion of molecules: 
- average kinetic energy of translational motion of molecules. We see that the value kT is a measure of the energy of thermal motion of molecules.
Gas laws were established experimentally in the 17th century. However, they can be obtained using the Mendeleev-Clapeyron equation.
Boyle-Marriott law. For a given amount of substance, consider isothermal process , that is, a process that occurs without a change in temperature (T = const). Using equation (2.6) or (2.7), we obtain the isotherm equation expressed in terms of gas pressure and volume: (2.7). or (2.7’). For a given amount of substance in an isothermal process, the product of pressure and volume is a constant value. To construct the P(V) diagram, we express the pressure in terms of volume. The relationship between pressure and volume is inversely proportional, graphically represented by a hyperbola in Fig. 2.3 A. Temperature dependences of pressure and volume are presented in Fig. 2.3 b And V, respectively.
Gay-Lussac's law. isobaric process , that is, a process that occurs without a change in pressure
(P = const). Using equation (2.6) or (2.7), we obtain the isobar equation expressed in terms of temperature and volume: ,(2.8). through the initial and final state parameters or . For a given amount of substance in an isobaric process, the ratio of volume to temperature (or vice versa) is a constant value.
The isobaric law can also be written in the form: . Here V 0 is the volume of gas at t = 0 0 C, t is the temperature at 0 C, a is the thermal coefficient of volumetric expansion; 
. For an ideal gas , , but , then - the thermal coefficient of volumetric expansion of an ideal gas is equal to the reciprocal of the temperature. An image of this process is shown in Fig. 2.4. Charles's law.
For a given amount of substance, consider isochoric process
, that is, a process that occurs without a change in volume (V = const). Using equation (2.6) or (2.7), we obtain the isochore equation expressed in terms of gas temperature and pressure: , (2.9) in terms of the initial and final state parameters or . For a given amount of substance in an isochoric process, the ratio of pressure to temperature (or vice versa) is a constant value.
An image of this process is shown in Fig. 2.5.
Avogadro's law At equal pressures (P) and temperatures (T), equal volumes (V) of any gas contain the same number of molecules. , therefore, N 1 = N 2
Dalton's law(for a mixture of gases) The pressure of a mixture of gases is equal to the sum of the partial pressures P cm = P 1 + P 2 +... + P K (2.10). This law can also be obtained using the ideal gas equation of state. 
, 
- partial pressure
- the pressure that a given gas component would exert if it alone occupied the entire volume provided by the mixture.
R - Numerically equal to the work of expansion of one mole of an ideal gas in an isobaric process with an increase in temperature by 1 K. = 8.31 J/(mol*K)
Sphere. , , the number of impacts on the wall in 1 s, therefore, the sum of all impulses communicated by one molecule in 1 s is equal to and for us such molecules i.e. the sum of impulses imparted to the wall by all molecules in 1 s, the force with which all molecules press on the wall. , root mean square speed of one molecule
, is the average kinetic energy of one molecule. : 
- Boltzmann constant
28. Maxwell's molecular velocity distribution. The most probable speed. Maxwell's law for the distribution of molecules of an ideal gas according to the speeds and energies of thermal motion When deriving the basic equation of molecular kinetic theory, the molecules were given different speeds. As a result of multiple collisions, the speed of each molecule changes in magnitude and direction. However, due to the chaotic movement of molecules, all directions of movement are equally probable, that is, on average, the same number of molecules moves in any direction. According to the molecular kinetic theory, no matter how the speeds of molecules change during collisions, the root mean square speed of molecules with mass m 0 in a gas in a state of equilibrium at T = const, remains constant and equal 
From (44.1) it is clear that the specific form of the function depends on the type of gas (on the mass of the molecule) and on the state parameter (on temperature T). The graph of function (44.1) is shown in Fig. 65. Since when increasing v factor 
decreases faster than the multiplier increases v2, then the function f(v), starting from zero, reaches a maximum at v in and then asymptotically tends to zero. The curve is asymmetrical with respect to v c. Relative number of molecules dN(v)/N, whose speeds lie in the range from v before v+dv, is found as the area of the lighter strip in Fig. 65. Area limited by the distribution curve 
and the x-axis is equal to one. This means that the function f(v) satisfies the normalization condition 
The speed at which the speed distribution function of ideal gas molecules is maximum is called the most probable speed. The value of the most probable speed can be found by differentiating expression (44.1) (we omit constant factors) with respect to the argument v, equating the result to zero and using the condition for the maximum of the expression f(v): 
Values v= 0i v=¥ correspond to the minima of expression (44.1), and the value v, at which the expression in brackets becomes equal to zero, and is the desired most probable speed v in: 
From formula (44.2) it follows that with increasing temperature, the maximum of the molecular velocity distribution function (Fig. 66) will shift to the right (the value of the most probable velocity becomes larger). However, the area limited by the curve remains unchanged, therefore, as the temperature increases, the molecular velocity distribution curve will stretch and decrease. Average molecular speed
29. Number of degrees of freedom. Boltzmann's law. Internal energy of gas. An important characteristic of a thermodynamic system is its internal energyU- the energy of chaotic (thermal) movement of microparticles of the system (molecules, atoms, electrons, nuclei, etc.) and the energy of interaction of these particles. From this definition it follows that internal energy does not include the kinetic energy of motion of the system as a whole and the potential energy of the system in external fields. Internal energy - single-valued function thermodynamic state of the system, i.e. in each state the system has a completely definite internal energy (it does not depend on how the system came to this state). This means that when a system transitions from one state to another, the change in internal energy is determined only by the difference in the values of the internal energy of these states and does not depend on the transition path. In § 1, the concept of the number of degrees of freedom was introduced - the number of independent variables (coordinates) that completely determine the position of the system in space. In a number of problems, a molecule of a monatomic gas (Fig. 77, a) is considered as a material point to which three 
degrees of freedom of translational motion. In this case, the energy of rotational motion can be ignored (r->0, J= mr 2 ®0, T vr =Jw 2 /2®0). In classical mechanics, a molecule of a diatomic gas is considered to a first approximation as a set of two material points rigidly connected by a non-deformable bond (Fig. 77b). In addition to three degrees of freedom of translational motion, this system has two more degrees of freedom of rotational motion. Rotation around the third axis (the axis passing through both atoms) is meaningless. Thus, a diatomic gas has five degrees of freedom (i=5). Triatomic (Fig. 77.0) and polyatomic nonlinear molecules have six degrees of freedom: three translational and three rotational. Naturally, there is no rigid connection between atoms. Therefore, for real molecules it is also necessary to take into account the degrees of freedom of vibrational motion. Regardless of the total number of degrees of freedom of molecules, the three degrees of freedom are always translational. None of the translational degrees of freedom has an advantage over the others, so each of them accounts for on average the same energy, equal to 1/3 of the value 
Where i- the sum of the number of translational, the number of rotational and twice the number of vibrational degrees of freedom of the molecule: i =i post + i rotate +2 i oscillation The classical theory considers molecules with rigid bonds between atoms; for them i coincides with the number of degrees of freedom of the molecule. Since in an ideal gas the mutual potential energy of the molecules is zero (the molecules do not interact with each other), the internal energy per one mole of gas will be equal to the sum of the kinetic energies N A of the molecules: 
Internal energy for an arbitrary mass T gas 
Where M - molar mass, v - amount of substance.
MOLECULAR PHYSICS
FUNDAMENTALS OF MOLECULAR KINETIC THEORY
1. Basic principles of molecular kinetic theory, the structure of matter from the point of view of MKT.
2. What is called an atom? A molecule?
3. What is the amount of a substance called? What is its unit (give definition)?
4. What is called molar mass and molar volume?
5. How can you determine the mass of molecules; molecular size. Approximately what is the mass of the molecules and their sizes?
6. Describe the experiments confirming the main provisions of MCT.
7. What is called an ideal gas? What conditions must it satisfy? Under what conditions is a real gas close in its properties to it?
8. Write down the formulas for arithmetic mean speed, root mean square speed.
9. What do diffusion experiments prove? Brownian motion? Explain them based on ICT
10. What does Stern’s experiment prove? Explain based on MCT.
11. Derive and formulate the basic MKT equation. What assumptions are used when deriving the basic MKT equation.
12. What does body temperature characterize?
13. Formulation and mathematical notation of the laws of Dalton, Boyle Mariotte, Gay Lussac, Charles.
14. What is the physical essence of absolute zero temperature? Write down the relationship between absolute temperature and temperature on the Celsius scale. Is absolute zero achievable and why?
15. How to explain gas pressure from the point of view of MCT? What does it depend on?
16. What does Avogadro's constant show? What is its value?
17. What is the value of the universal gas constant?
18. What is the value of Boltzmann's constant?
19. Write the Mendeleev – Clapeyron equation. What quantities are included in the formula?
20. Write the Clapeyron equation. What quantities are included in the formula?
21. What is the partial pressure of a gas?
22. What is called an isoprocess, what isoprocesses do you know.
23. Concept, definition, internal energy of an ideal gas.
24. Gas parameters. Derivation of the unified gas law.
25. Derivation of the Mendeleev-Clapeyron equation.
26. What is called: molar mass of a substance, amount of a substance, relative atomic mass of a substance, density, concentration, absolute temperature of a body? In what units are they measured?
27. Gas pressure. SI units of pressure. Formula. Instruments for measuring pressure.
28. Describe and explain two temperature scales: thermodynamic and practical.
30. Formulate laws that describe all types of isoprocesses?
31. Draw a graph of the density of an ideal gas versus thermodynamic temperature for an isochoric process.
32. Draw a graph of the density of an ideal gas versus thermodynamic temperature for an isobaric process.
33. How does the Clapeyron-Mendeleev equation differ from the Clapeyron equation?
34. Write down the formula for the average kinetic energy of an ideal gas.
35. Mean square speed of thermal motion of molecules.
36. Average speed of chaotic movement of molecules.
2. The particles that make up substances are called molecules. The particles that make up molecules are called atoms.
3. The quantity that determines the number of molecules in a given sample of a substance is called the amount of substance. One mole is the amount of a substance that contains as many molecules as there are carbon atoms in 12 g of carbon.
4. Molar mass of a substance - the mass of one mole of a substance (g/mol) Molar volume - the volume of one mole of a substance, the value obtained by dividing the molar mass by the density.
5. Knowing the molar mass, you can calculate the mass of one molecule: m0 = m/N = m/vNA = M/NA The diameter of a molecule is considered to be the minimum distance at which repulsive forces allow them to approach each other. However, the concept of molecular size is relative. The average size of molecules is about 10-10 m.
7. An ideal gas is a model of a real gas that has the following properties:
Molecules are negligible compared to the average distance between them
The molecules behave like small hard balls: they elastically collide with each other and with the walls of the vessel, there are no other interactions between them.
Molecules are in constant chaotic motion. All gases at not too high pressures and at not too low temperatures are close in their properties to an ideal gas. At high pressures, gas molecules come so close together that their own sizes cannot be neglected. As the temperature decreases, the kinetic energy of molecules decreases and becomes comparable to their potential energy; therefore, at low temperatures, potential energy cannot be neglected.
At high pressures and low temperatures, the gas cannot be considered ideal. This gas is called real.(The behavior of a real gas is described by laws that differ from the laws of an ideal gas.)
The root mean square speed of molecules is the root mean square value of the velocity modules of all molecules of the considered amount of gas
And if we write the universal gas constant as , and for one molar mass, then we will succeed?
In the Formula we used:
Mean square speed of molecules
Boltzmann's constant
Temperature
Mass of one molecule
Universal gas constant
Molar mass
Quantity of substance
Average kinetic energy of molecules
Avogadro's number
The arithmetic average speed of molecules is determined by the formula
Where M - molar mass of a substance.
9. Brownian motion. One day in 1827, the English scientist R. Brown, while studying plants using a microscope, discovered a very unusual phenomenon. Spores floating on the water (small seeds of some plants) moved spasmodically for no apparent reason. Brown observed this movement (see picture) for several days, but could not wait for it to stop. Brown realized that he was dealing with a phenomenon unknown to science, so he described it in great detail. Subsequently, physicists named this phenomenon after the name of its discoverer - Brownian movement.
It is impossible to explain Brownian motion unless assume that water molecules are in random, never-ending motion. They collide with each other and with other particles. When the molecules encounter spores, they cause them to move spasmodically, which Brown observed under a microscope. And since molecules are not visible under a microscope, the movement of the spores seemed to Brown to be causeless.
Diffusion
 |
How can we explain the acceleration of these phenomena? There is only one explanation: An increase in body temperature leads to an increase in the speed of movement of its constituent particles.
So, what are the conclusions from the experiments? The independent movement of particles of substances is observed at any temperature. However, as the temperature increases, the movement of particles accelerates, which leads to an increase in their kinetic energy. As a result, these more energetic particles speed up diffusion, Brownian motion, and other phenomena such as dissolution or evaporation.
10. Stern experience- an experiment in which the speed of molecules was experimentally measured. It has been proven that different molecules in a gas have different speeds, and at a given temperature we can talk about the distribution of molecules by speed and the average speed of molecules.
Examples of problem solving. 1.3.1. The root mean square speed of some gas molecules is 450 m/s
1.3.1. The root mean square speed of some gas molecules is 450 m/s. Gas pressure 50 kPa. Find the gas density under these conditions.
Solution. The root mean square speed of gas molecules is related to its temperature by the relation
where R is the universal gas constant;
m is the molecular mass of the gas;
T – absolute gas temperature.
To determine the gas temperature, we use the Mendeleev-Clapeyron equation
where r=m/V is the gas density.
Hence
.
Substituting numerical values we have
1.3.2. Find the average free path of air molecules under normal conditions. The effective diameter of air molecules is s=0.3 nm.
Solution. Mean free path of gas molecules
,
Where
s is the effective diameter of the molecule;
n – number of molecules per unit volume (concentration of molecules). To determine the number of molecules per unit volume, we use the basic equation of molecular kinetic theory for pressure
where k is Boltzmann’s constant;
T – gas temperature.
Then for the mean free path we have
.
Substituting the numerical values, we finally get:
m.
1.3.3. Find the average number of collisions per unit time of carbon dioxide molecules at a temperature of 100 o C, if the average free path
Solution. The number of collisions of gas molecules per unit time is related to the mean free path by the relation
,
Where 
– arithmetic average speed.
Hence,
Substituting the numerical values we have
1.3.4. At a certain pressure and temperature of 0 o C, the average free path of oxygen molecules is 95 nm. Find the average number of collisions per unit time of oxygen molecules if the oxygen pressure is reduced by a factor of 100.
Solution. Average number of collisions per unit time
,
Where
When the gas pressure changes, the mean free path is inversely proportional to the pressure:
,
where l 1, l 2 is the free path of gas molecules at the corresponding pressures p 1 and p 2.
In our case:
Substituting numerical values for
1.3.5. What part of oxygen molecules at t=0 o C has velocities from 100 to 110 m/s?
Solution. The velocity distribution of molecules can be determined from Maxwell's law
,
where u=v/v in – relative speed;
v – given speed;
v in =(2RT/m) 1/2 – the most probable speed of molecules;
Du is the interval of relative speeds, small compared to the speed u.
Then the required part of the molecules that needs to be determined (distribution of molecules by speed)
In our case v=100 m/s; v=10 m/s; The most probable speed is v=(2RT/pm) 1/2 =376 m/s. Therefore, u=v/v in =100/376, u 2 =0.071; Du=10/376; exp(-u 2)=0.93.
Thus, the number of oxygen molecules whose velocities lie in the indicated interval is equal to 4% of the total number of molecules.
1.3.6. A container containing gas moves at speed v o and then quickly stops. How much will the average square of the speed of thermal motion of gas molecules increase in the case of a monatomic gas? Diatomic gas? Gas is considered ideal.
Solution. Let's use the law of conservation of energy. Let M be the mass of gas in the container. Moving at speed v, the gas as a whole has kinetic energy
W k = Mv o 2 /2.
This formula determines the kinetic energy of the directional movement of molecules in which they participate together with the vessel. After the vessel stops, the directed movement of molecules as a result of their collisions with the walls of the vessel will very soon turn into chaotic.
Neglecting the heat exchange between the gas and the walls of the vessel over the period of time under consideration, the gas can be considered an isolated system. Then from the law of conservation of energy it follows that the “disappeared” kinetic energy of the directed motion of molecules W must be equal to the increase in the energy of chaotic motion of molecules (increase in internal energy DU:
Let us determine the internal energy of the gas. For an ideal monatomic gas, this is the energy of the translational chaotic motion of molecules:
where m is the mass of the molecule;
N is the number of molecules in the vessel.
It follows that the change in the internal energy of a monatomic gas during braking
DU=U 2 –U 1 =M/2,
where v kv1, v kv2 are the root mean square velocities of gas molecules at the beginning and end of braking, respectively.
Substituting the values of W k and DU into the equation W k =DU, we get the first answer
v 2 sq2 -v 2 sq1 =v 2 o.
The internal energy of an ideal diatomic gas consists of the energies of translational and rotational motion of molecules. In this case, three degrees of freedom are for translational motion and two for rotational motion. In accordance with the law of uniform distribution of energy across degrees of freedom, three-fifths of the kinetic energy W will go to increase the energy of translational motion of molecules and two-fifths will go to increase the energy of their rotational motion. Thus, we now have
Where do we get the second answer:
1.3.7. What fraction of hydrogen molecules at temperature T have velocities that differ from the most probable velocity by no more than 5.0 m/s? Solve the problem for two values of T: 1) 400 K, 2) 900 K.
Solution. The distribution of molecules by speed is expressed by Maxwell's law: the number of molecules DN, the relative speeds of which lie in the range from u to u+Du:
where N is the total number of gas molecules;
– Maxwell distribution function;
u=v/v in – relative speed;
v – given speed;
v in – the most probable speed.
Maxwell's distribution law turns out to be valid under the condition Du From here we find that part of the molecules whose relative velocities lie in the interval Du: Before making calculations, you must make sure that the condition Du To calculate Du, we first find the most probable speed at T=400 K and T=900 K using the formula: v in1 =2×8.31×400/0.002=1.82×10 3 m/s, v v2 =2×8.31×900/0.002=2.73×10 3 m/s. Substituting these values of v in and keeping in mind that Dv = 10 m/s, since the problem is about velocities lying in the range from v in = -5.0 m/s to v in = +5.0 m/s , we get: Du 1 =1/182, Du 2 =1/273. Since u=1, we see that the condition Du
Now let's find DN 1 /N=4/((3.14) 1/2 ×2.7×182)=0.0046, DN 2 /N=4/((3.14) 1/2 ×2.7×273)=0.0030. Thus, as the temperature increases, the most probable speed of molecules increases, and the number of molecules whose speeds lie in the same interval around the most probable speed decreases. Mean square speed of molecules - root mean square value of the velocity modules of all molecules of the considered amount of gas Table of values of the root mean square speed of molecules of some gases In order to understand where we get this formula from, we will derive the root mean square speed of the molecules. The derivation of the formula begins with the basic equation of molecular kinetic theory (MKT): Where we have the amount of substance, for easier proof, let’s take 1 mole of substance for consideration, then we get: If you look, PV is two-thirds of the average kinetic energy of all molecules (and we take 1 mole of molecules): Then, if we equate the right-hand sides, we get that for 1 mole of gas the average kinetic energy will be equal to: But the average kinetic energy is also found as: But now, if we equate the right-hand sides and express the speed from them and take the square, Avogadro’s Number per molecule mass, we get Molar mass, then we get a formula for the root mean square speed of a gas molecule: And if we write the universal gas constant as , and for one molar mass, then we will succeed? In the Formula we used: Mean square speed of molecules Boltzmann's constant
.
